Wolfram Alpha Screenshot tour

Wolfram|Alpha is a computable search engine. That is to say, while it has large amounts of stored information its real value lies in its ability to work with that information. It has just yesterday been released to the public and for such an anticipated project the launch was carried through with very little in the way of problems (discussed below). Wolfram Alpha is by the same people behind the great mathematics software package Mathematica, and uses Mathematica for its computations. Some of the screenshots below come from the sample inputs, and if you are unsure of what to ask, Wolfram|Alpha's homepage has some great suggestions. Without further ado, let the screenshots begin.

Wolfram|Alpha can integrate. This is not a big feature to those familiar with the Wolfram Integrator, however Wolfram|Alpha will show its work for most indefinite integrals and derivatives:

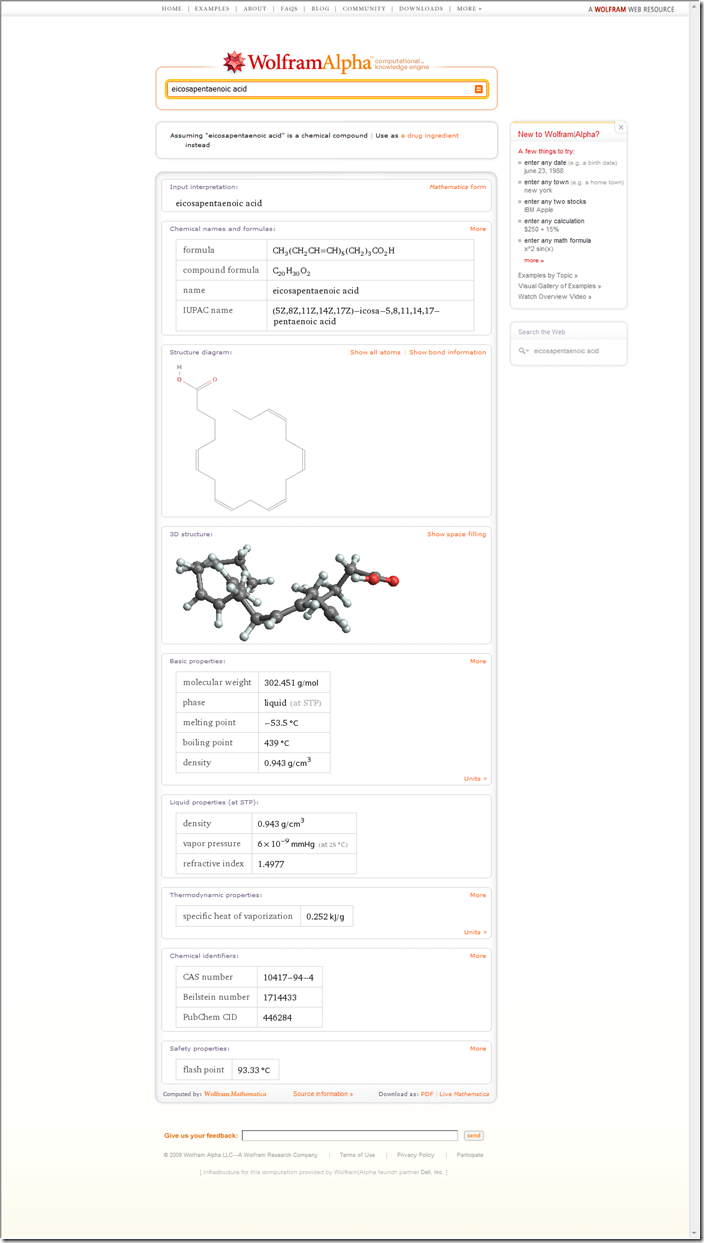
It can identify chemicals and give their formulas, names, structures, 3d diagrams, and properties.

It also features a differential equation solver:

These are just a few examples of what Wolfram|Alpha can do. Sometimes, though, it runs into one of the launch quirks mentioned above:

(Failed screenshot from Gizmodo, usually just refreshing several times will get the error to go away)

Other occasional problems include Wolfram|Alpha misinterpreting input or there not being any information on a particular topic in Wolfram|Alpha's database, as it is all source-checked and added by hand (or by computers but checked by people).

Most commonly misinterpretation is due to the user not being specific, however sometimes it just does not know what to do with an input. In this case, it does not understand that the properties of a 1 molar solution of hydrochloric acid are being requested, but it does offer some interesting (and somewhat helpful) suggestions.

Some of the more interesting things that can be done with Wolfram|Alpha include language comparisons:

Searching for gene sequences through the entire human genome:

Comparing countries:

and comparing elements:

Below each data section there is usually an option to add more data to the display, and at the bottom (depends on what browser you use, Chrome didn't work for me but Opera and Internet Explorer did) there is an option to export either to a Mathematica notebook or to a pdf, however currently exporting to a pdf does not include the "more" data that has been selected.

Wolfram|Alpha also can tell you what a certain measurement equals in terms that are easier to understand.

 

Wolfram|Alpha is a great tool for research, public data searching, and computation. Many of its results (such as those on planetary motions) are computed for the exact moment that you asked the question. Its provides sources for much of the raw data used in its computations, making it an easily cited source. It also contains many health studies, and can provide information on correlations between various pieces of data. It is an excellent tool, and I look forward to the few problems it has being fixed in the near future.